Extending and comparing methods for synthetic social contact matrices

SPECTRUM & SPARK Annual Meeting

Nicholas Tierney

Telethon Kids Institute

15th Feb, 2023

A contact matrix

• If we know how many times people have contact, we have an idea of which age groups will spread COVID

• Simulate how many COVID cases would get transmitted

• Explore how vaccination reduces transmission

• Do this for different areas in Australia

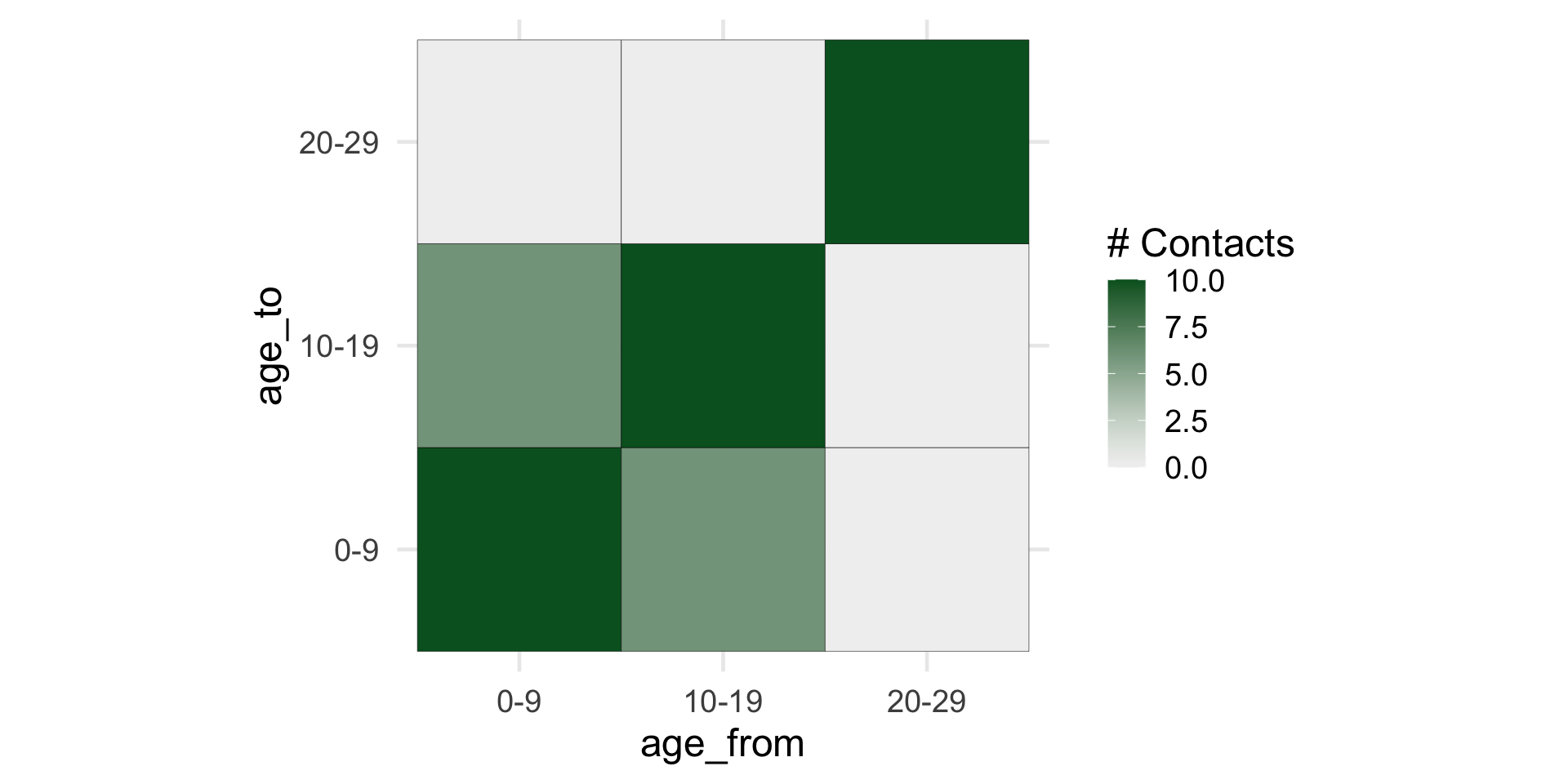
Mossong et al (POLYMOD)

Prem et al - Synthetic Contact Matrices

image of spreadsheet booklet of contact matrices

The main issue with this is that we don’t have much control over the outputs.

And maybe that doesn’t matter to you if you just need to look at the contact matrices for a given country.

But what we needed to do is get contact matrices for a given age population structure.

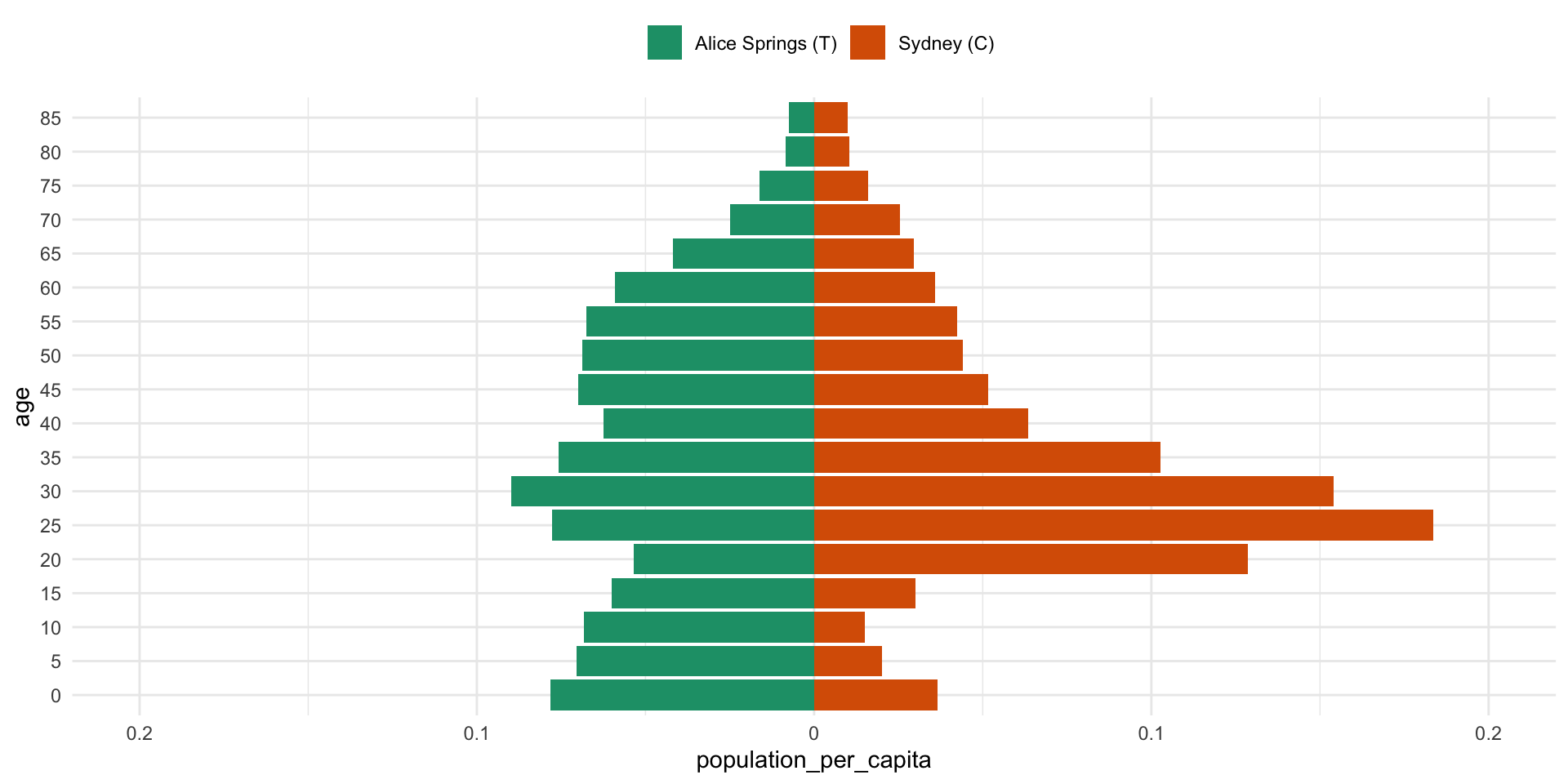
Populations are different

Key points

• Contact matrices can model infectious disease spread
• We need contact matrices for specific parts of Australia
• Current best estimates are for all of Australia
• We need our own approach

• POLYMOD: empirical contact data for 8 countries

• Prem et al extrapolated POLYMOD to 155 countries

• Prem matrices were very widely adopted

• Various improvements can be made to Prem et al

• Prem’s updated matrices: Australia & NZ not included

• We needed finer grained Australian contact matrices

We need an R package: conmat

• Input: age population data
• Output: synthetic contact matrix
• Provide tools to:
  • Create next generation matrices
  • Apply vaccination
  • Use these in SIR modelling

Age population data

library(conmat)
fairfield <- abs_age_lga("Fairfield (C)")
fairfield

# A tibble: 18 × 4 (conmat_population)
 - age: lower.age.limit
 - population: population
   lga           lower.age.limit  year population
   <chr>                   <dbl> <dbl>      <dbl>
 1 Fairfield (C)               0  2020      12261
 2 Fairfield (C)               5  2020      13093
 3 Fairfield (C)              10  2020      13602
 4 Fairfield (C)              15  2020      14323
 5 Fairfield (C)              20  2020      15932
 6 Fairfield (C)              25  2020      16190
 7 Fairfield (C)              30  2020      14134
 8 Fairfield (C)              35  2020      13034
 9 Fairfield (C)              40  2020      12217
10 Fairfield (C)              45  2020      13449
11 Fairfield (C)              50  2020      13419
12 Fairfield (C)              55  2020      13652
13 Fairfield (C)              60  2020      12907
14 Fairfield (C)              65  2020      10541
15 Fairfield (C)              70  2020       8227
16 Fairfield (C)              75  2020       5598
17 Fairfield (C)              80  2020       4006
18 Fairfield (C)              85  2020       4240

Predict (extrapolate) a new contact matrix

synthetic_fairfield <- extrapolate_polymod(
 population = fairfield,
 age_breaks = c(seq(0, 75, by = 5), Inf) # default
)

synthetic_fairfield

── Setting Prediction Matrices ────────────

A list of matrices containing the model
predicted contact rate between ages in
each setting.

• home: a 16x16 <matrix>
• work: a 16x16 <matrix>
• school: a 16x16 <matrix>
• other: a 16x16 <matrix>
• all: a 16x16 <matrix>
ℹ Access each <matrix> with `x$name`
ℹ e.g., `x$home`

Synthetic Contact matrix

autoplot(synthetic_fairfield$home)

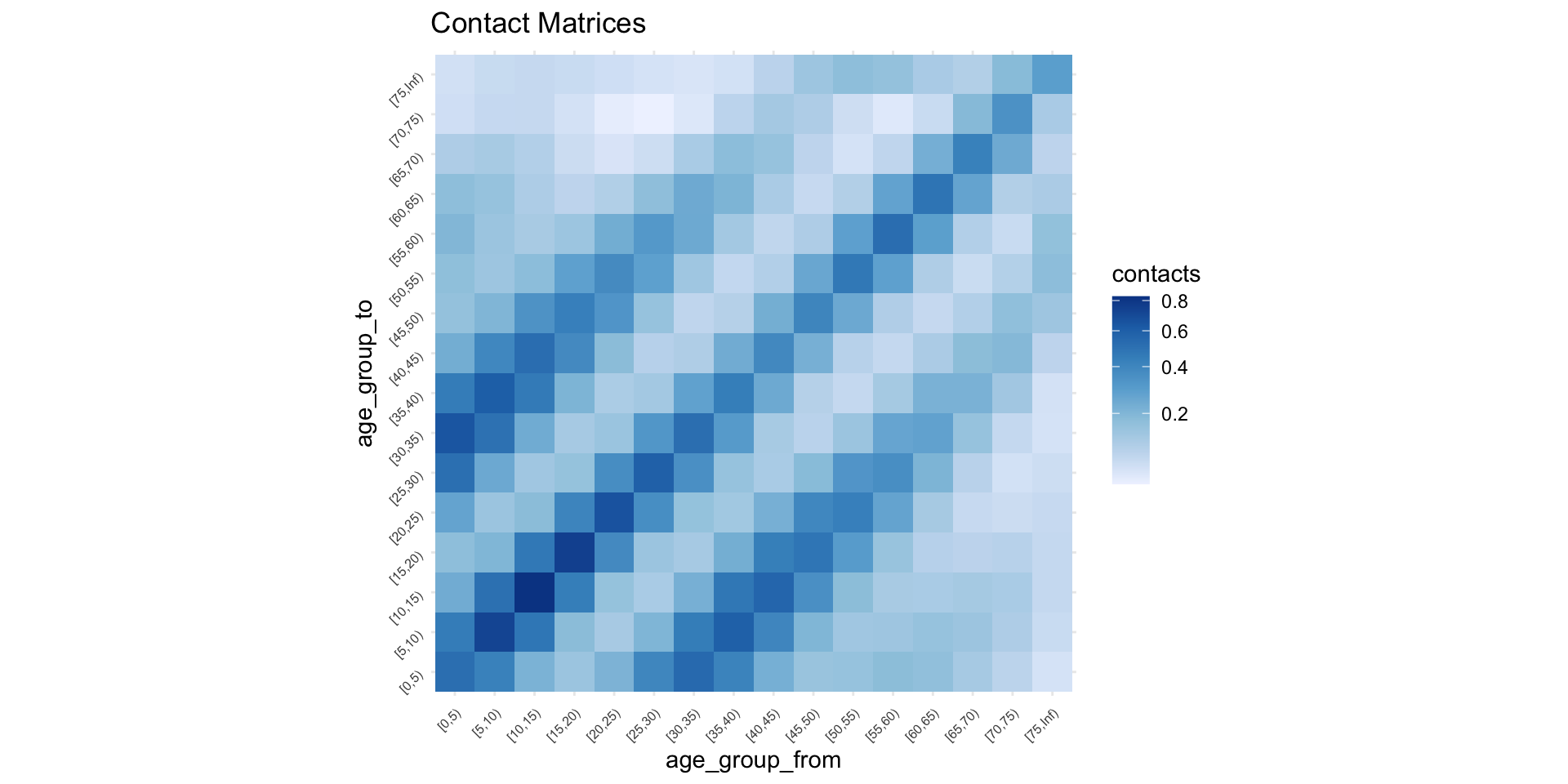
Next Generation Matrix

fairfield_ngm <- generate_ngm(
  synthetic_fairfield,
  age_breaks = c(seq(0, 75, 5), Inf),
  R_target = 1.5
  )

fairfield_ngm

── NGM Setting Matrices ──────────────────

A list of matrices, each <matrix>
containing the number of newly infected
individuals for a specified age group.

• home: a 16x16 <matrix>
• school: a 16x16 <matrix>
• work: a 16x16 <matrix>
• other: a 16x16 <matrix>
• all: a 16x16 <matrix>
ℹ Access each <matrix> with `x$name`
ℹ e.g., `x$home`

Next Generation Matrix

autoplot(fairfield_ngm$home)

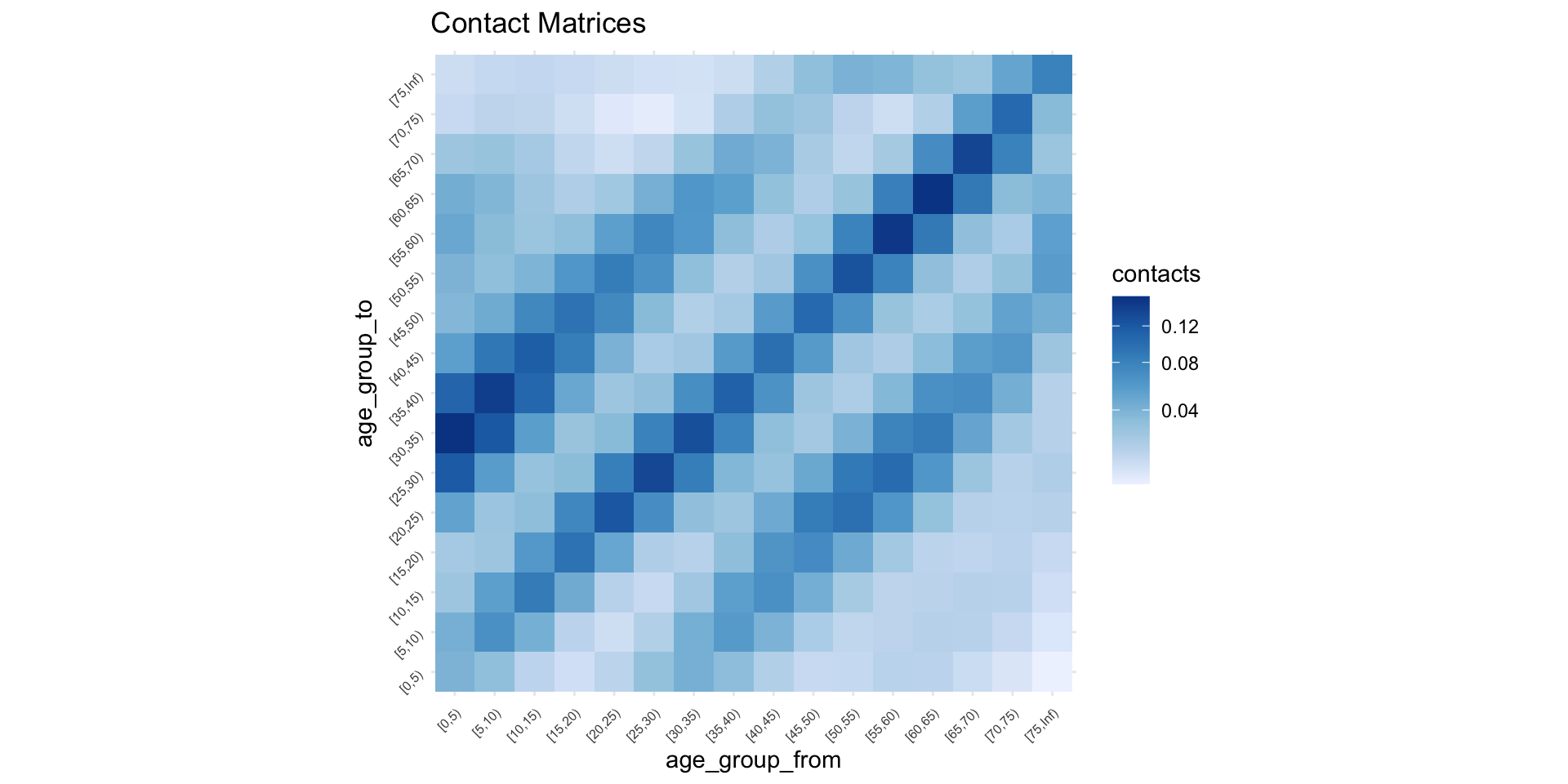
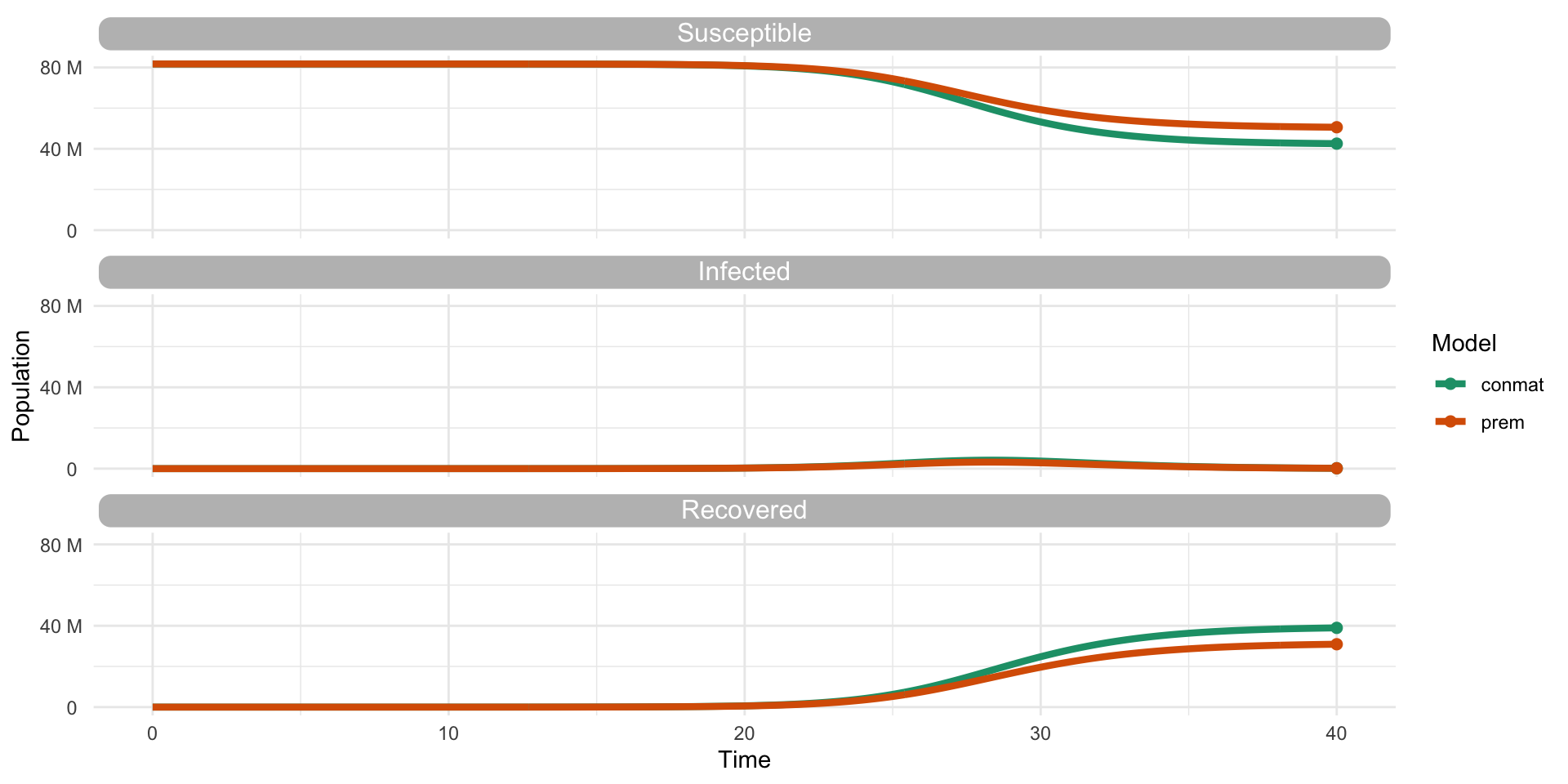
But is it different to Prem?

• Compare our contact matrix to Prem’s contact matrix
• In a Suscepible, Infected, Recovered (SIR) model
• For say, Germany?

…Is it different to Prem?

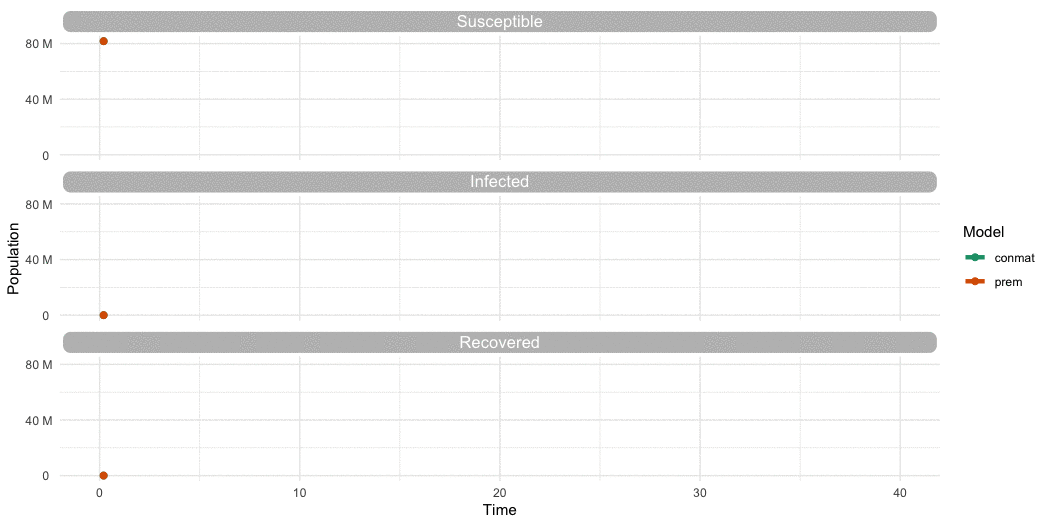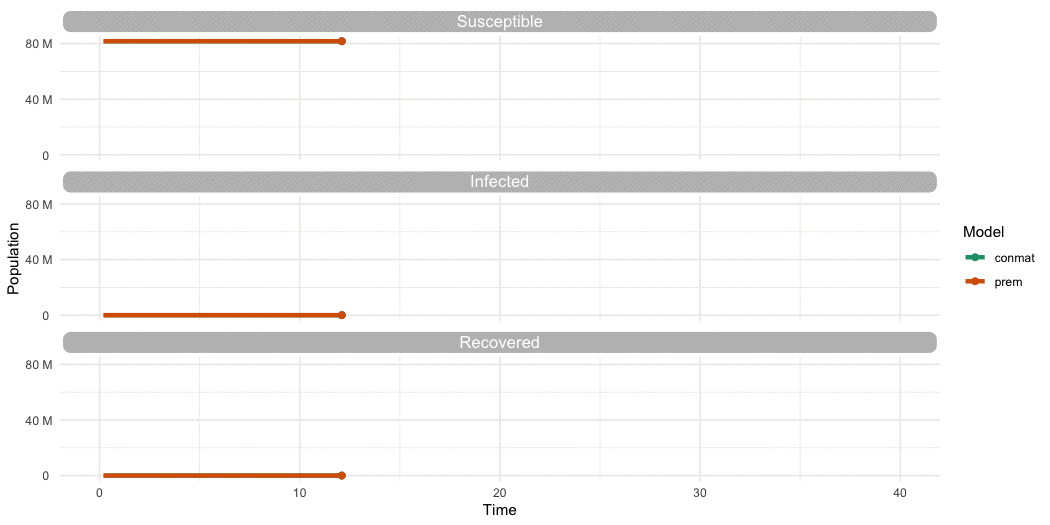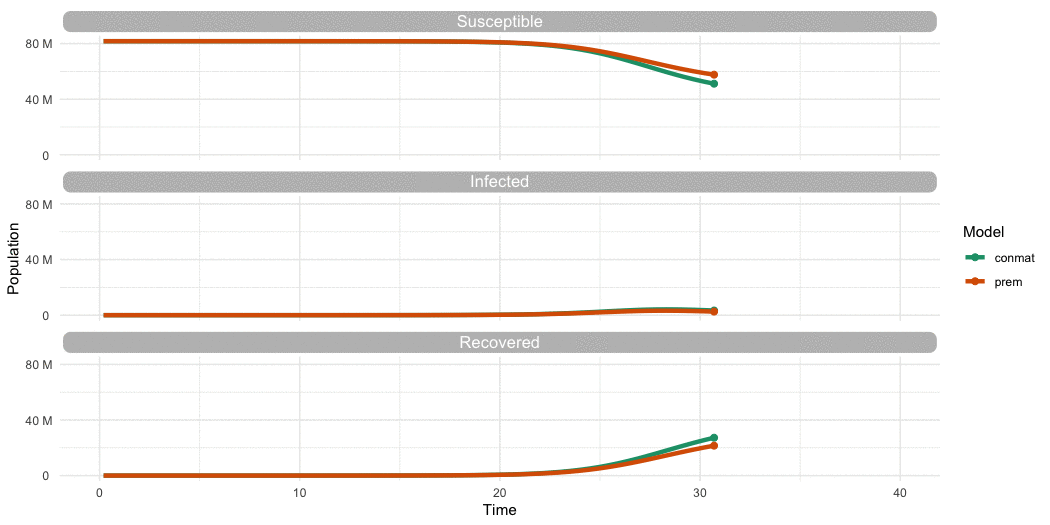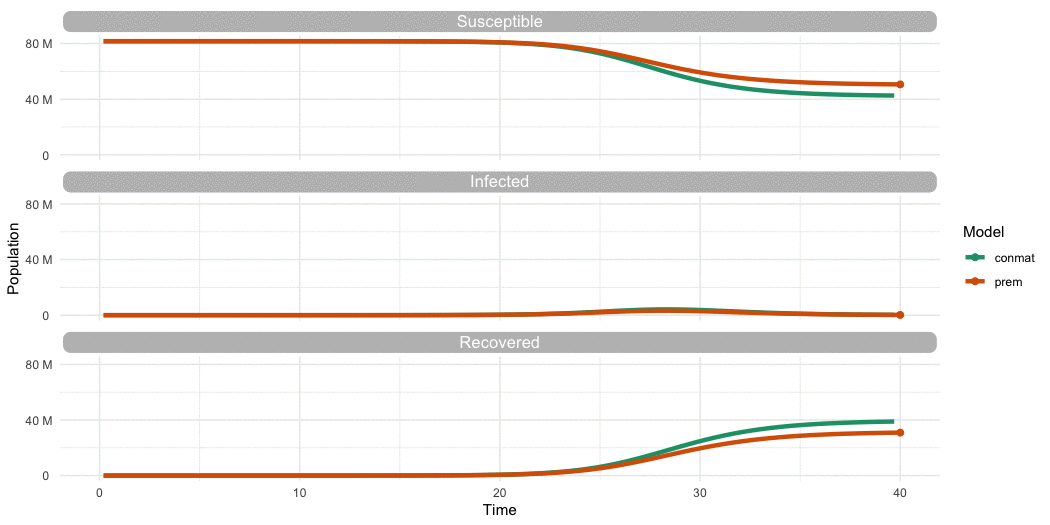
…Yes

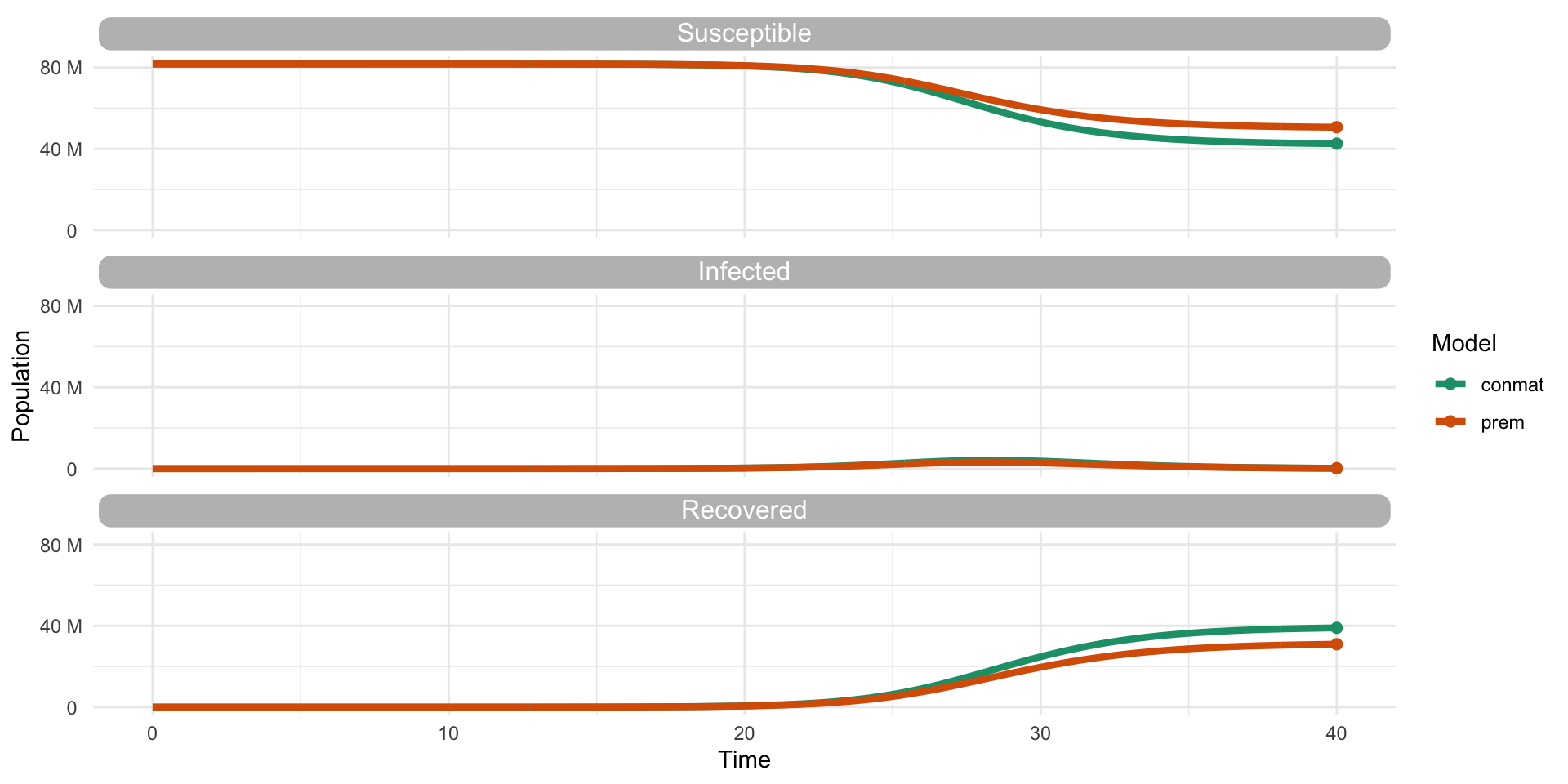
…Yes (but we need to look further)

Thanks

• Nick Golding
• Aarathy Babu
• Michael Lydeamore
• Spark Spectrum Seed Funding

Learning more

github.com/njtierney/conmat

github.com/njtierney/talk-spark-2023

njtierney.com

njtierney@aus.social

nj_tierney

njtierney

nicholas.tierney@gmail.com

End.

Extras

Next Generation Matrices

• Once infected, a person can transmit an infectious disease to another, creating generations of infected individuals.
• We can define a matrix describing the number of newly infected individuals in age groups, for consecutive generations.
• This matrix is called a next generation matrix (NGM).

Apply Vaccination

• Applies the effect of vaccination on the next generation of infections, to understand and describe the reduction of acquisition and transmission in each age group.

• Takes the following arguments:

  • ngm - a Next Generation Matrix
  • data - A data frame with location specifics
  • which columns are related to “coverage”, “acquisition”, and “transmission” in the data col

Example vaccination data

vaccination_effect_example_data

# A tibble: 17 × 4
   age_band coverage acquisition transmission
   <chr>       <dbl>       <dbl>        <dbl>
 1 0-4         0           0            0    
 2 5-11        0.782       0.583        0.254
 3 12-15       0.997       0.631        0.295
 4 16-19       0.965       0.786        0.469
 5 20-24       0.861       0.774        0.453
 6 25-29       0.997       0.778        0.458
 7 30-34       0.998       0.803        0.493
 8 35-39       0.998       0.829        0.533
 9 40-44       0.999       0.841        0.551
10 45-49       0.993       0.847        0.562
11 50-54       0.999       0.857        0.579
12 55-59       0.996       0.864        0.591
13 60-64       0.998       0.858        0.581
14 65-69       0.999       0.864        0.591
15 70-74       0.999       0.867        0.597
16 75-79       0.999       0.866        0.595
17 80+         0.999       0.844        0.556

I think they are the average vaccine efficacy (expressed as 1 minus the relative risk) over all vaccinated individuals in the population. I.e. we calculate an average form the number of people in that age group that have 1 dose, 2 doses, which brand, how long ago, etc.

Apply vaccination

ngm_vacc_fairfield <- apply_vaccination(
  ngm = ngm_fairfield,
  data = vaccination_effect_example_data,
  coverage_col = coverage,
  acquisition_col = acquisition,
  transmission_col = transmission
)

ngm_vacc_fairfield

── Vaccination Setting Matrices ──────────

A list of matrices, each <matrix>
containing the adjusted number of newly
infected individuals for age groups.
These numbers have been adjusted based on
proposed vaccination rates in age groups

• home: a 17x17 <matrix>
• school: a 17x17 <matrix>
• work: a 17x17 <matrix>
• other: a 17x17 <matrix>
• all: a 17x17 <matrix>
ℹ Access each <matrix> with `x$name`
ℹ e.g., `x$home`

How does the model work?

• Train a GAM predicting contact rate on POLYMOD data

• Simplified:

model <- mgcv::bam(
  contact ~ age_diagonal + 
     age_offdiagonal + 
     ... + 
     school probability + 
     work probability
  )

extrapolated <- predict(
  data = fairfield, 
  model = model
  )

How does the model work (really)?

(simplified)

mgcv::bam(
  formula = contacts ~
      # Prem method did a post-hoc smoothing
      # abs(age_from - age_to)
      s(gam_age_offdiag) +
      # abs(age_from - age_to)^2
      s(gam_age_offdiag_2) +
      # abs(age_from * age_to)
      s(gam_age_diag_prod) +
      # abs(age_from + age_to)
      s(gam_age_diag_sum) +
      # pmax(age_from, age_to)
      s(gam_age_pmax) +
      # pmin(age_from, age_to)
      s(gam_age_pmin) +
      school_probability +
      work_probability,
    family = stats::poisson,
    # NOTE: the offset of participants allows us to get the rate per person
    offset = log(participants),
    data = .
    )

How does the model work (really really)?

• Here’s the link to the code

Some Prem et al Limitations

• Although they provided the code:

• It was code not written for reuse (code vs software)

  • No interface on getting matrix for a specified region.
  • Unclear which code matched which methods

• Australia was in original 155 countries, not in the new updated 177!

This is the last slide.