Using Cross Validation with maxcovr

Nicholas Tierney

2019-06-13

This vignette provides a guide to performing cross validation with modelr and maxcovr. Cross validation is a bit of a strange concept in this context - we aren’t trying to make predictions here, but what we are trying to do is appropriately evaluate the performance of maxcovr in a fairer way.

In the future if this is a feature that is under demand, I will incorporate cross validation into maxcovr. In the mean time, here’s a vignette.

Performing cross validation on max_coverage

We will stick with the previous example using york and york_crime

library(maxcovr)
library(dplyr)

## 
## Attaching package: 'dplyr'

## The following objects are masked from 'package:stats':
## 
##     filter, lag

## The following objects are masked from 'package:base':
## 
##     intersect, setdiff, setequal, union

# subset to be the places with towers built on them.
york_selected <- york %>% filter(grade == "I")

york_unselected <- york %>% filter(grade != "I")

Thanks to the modelr package, it is relatively straightforward to perform cross validation.

# first we partition the data into 5 folds
library(modelr)
library(purrr)
library(tibble)
mc_cv <- modelr::crossv_kfold(york_crime, 5) %>% 
    # we change the test and train sets from the `resample`
    # to tibbles
    mutate(test = map(test,as_tibble),
           train = map(train,as_tibble))

This creates a dataframe with test and training sets

mc_cv

## # A tibble: 5 x 3
##   train                 test                .id  
##   <list>                <list>              <chr>
## 1 <tibble [1,451 × 12]> <tibble [363 × 12]> 1    
## 2 <tibble [1,451 × 12]> <tibble [363 × 12]> 2    
## 3 <tibble [1,451 × 12]> <tibble [363 × 12]> 3    
## 4 <tibble [1,451 × 12]> <tibble [363 × 12]> 4    
## 5 <tibble [1,452 × 12]> <tibble [362 × 12]> 5

We then fit the model on the training set using map_df, from the purrr package.

library(purrr)
# then we fit the model
system.time(
    mc_cv_fit <- map_df(mc_cv$train,
                     ~max_coverage(existing_facility = york_selected,
                                   proposed_facility = york_unselected,
                                   user = ., # training set goes here
                                   n_added = 20,
                                   distance_cutoff = 100))
)

##    user  system elapsed 
##   3.536   0.423   3.978

Then we can use the summary_mc_cv function to extract out the summaries from each fold. This summary takes the facilities placed using the training set of users, and then takes the test set of users and counts what percent of these are being covered by the training model.

summarised_cv <- summary_mc_cv(mc_cv_fit, mc_cv)

summarised_cv %>% knitr::kable()

n_added	n_fold	distance_within	n_cov	pct_cov	n_not_cov	pct_not_cov	dist_avg	dist_sd
20	1	100	58	0.1597796	305	0.8402204	1065.714	1382.361
20	2	100	45	0.1239669	318	0.8760331	1175.605	1604.221
20	3	100	37	0.1019284	326	0.8980716	1325.302	1703.502
20	4	100	53	0.1460055	310	0.8539945	1024.408	1341.573
20	5	100	49	0.1353591	313	0.8646409	1104.269	1310.461

Eyeballing the values, it looks like the pct coverage stays around 10%, but we can plot it to get a better idea. We can overlay the coverage obtained using the full dataset to get an idea of how we are performing.

library(ggplot2)
summarised_cv %>%
    ggplot(aes(x = n_fold,
               y = pct_cov)) + 
    geom_point() +
    geom_line(group = 1) + 
    theme_minimal()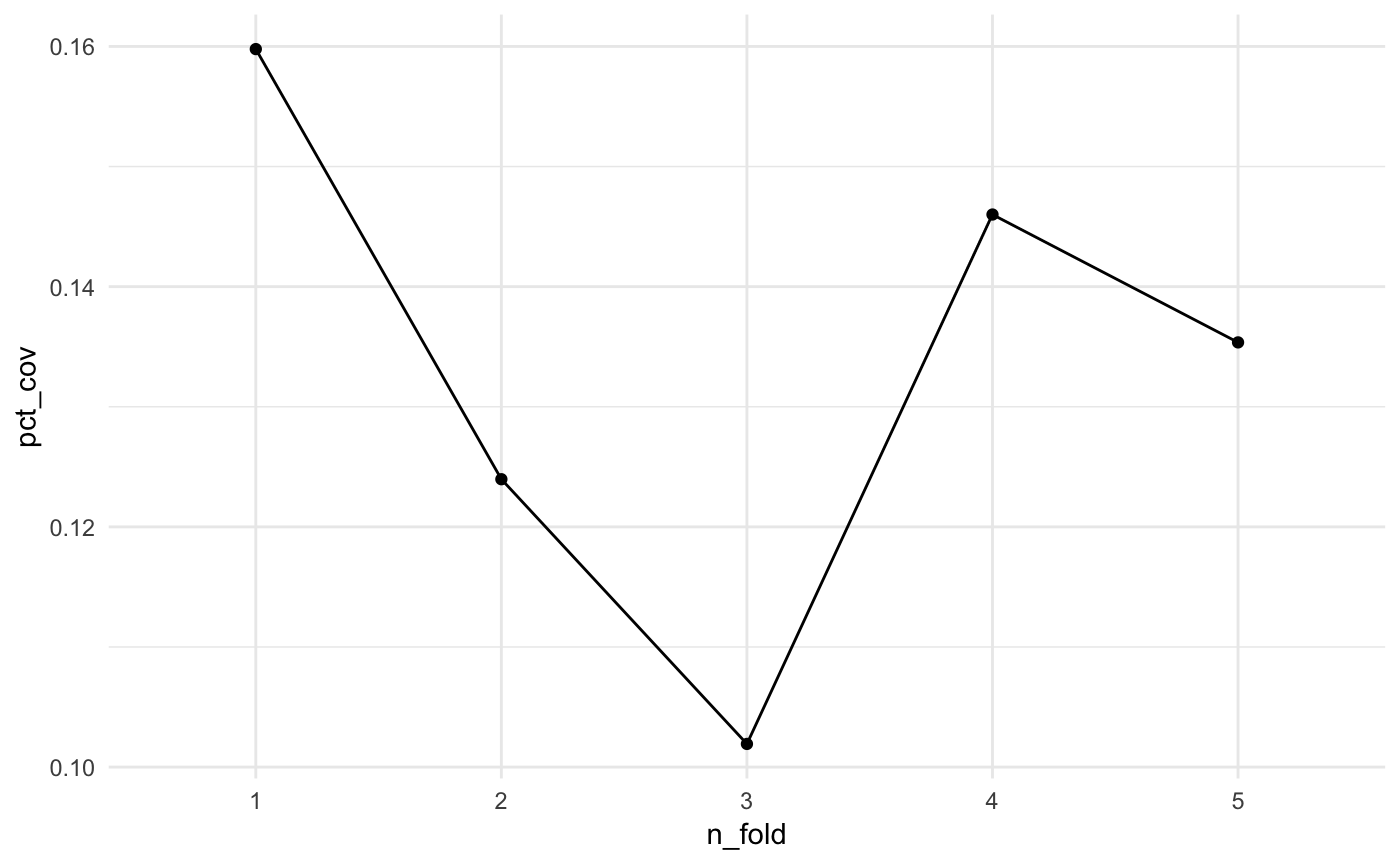

Here we see that the pct_coverage doesn’t seem to change much across the folds.

Coming up next, we will explore how to perform cross validation as we increase the number of facilities added.

Ideally, there should be a way to do this using purrr, so we don’t have to fic 5 separate models, but perhaps this will change when we enable n_added to take a vector of values.

# then we fit the model
system.time(
    mc_cv_fit_n20 <- map_df(mc_cv$train,
                     ~max_coverage(existing_facility = york_selected,
                                   proposed_facility = york_unselected,
                                   user = ., # training set goes here
                                   n_added = 20,
                                   distance_cutoff = 100))
)

##    user  system elapsed 
##   3.329   0.412   3.745

system.time(
    mc_cv_fit_n40 <- map_df(mc_cv$train,
                     ~max_coverage(existing_facility = york_selected,
                                   proposed_facility = york_unselected,
                                   user = ., # training set goes here
                                   n_added = 40,
                                   distance_cutoff = 100))
)

##    user  system elapsed 
##   3.400   0.332   3.739

system.time(
    mc_cv_fit_n60 <- map_df(mc_cv$train,
                     ~max_coverage(existing_facility = york_selected,
                                   proposed_facility = york_unselected,
                                   user = ., # training set goes here
                                   n_added = 60,
                                   distance_cutoff = 100))
)

##    user  system elapsed 
##   3.737   0.344   4.089

system.time(
    mc_cv_fit_n80 <- map_df(mc_cv$train,
                     ~max_coverage(existing_facility = york_selected,
                                   proposed_facility = york_unselected,
                                   user = ., # training set goes here
                                   n_added = 80,
                                   distance_cutoff = 100))
)

##    user  system elapsed 
##   3.665   0.453   4.124

system.time(
    mc_cv_fit_n100 <- map_df(mc_cv$train,
                     ~max_coverage(existing_facility = york_selected,
                                   proposed_facility = york_unselected,
                                   user = ., # training set goes here
                                   n_added = 100,
                                   distance_cutoff = 100))
)

##    user  system elapsed 
##  31.324   0.593  32.095

summarised_cv_n20 <- summary_mc_cv(mc_cv_fit_n20, mc_cv)
summarised_cv_n40 <- summary_mc_cv(mc_cv_fit_n40, mc_cv)
summarised_cv_n60 <- summary_mc_cv(mc_cv_fit_n60, mc_cv)
summarised_cv_n80 <- summary_mc_cv(mc_cv_fit_n80, mc_cv)
summarised_cv_n100 <- summary_mc_cv(mc_cv_fit_n100, mc_cv)

bound_testing_summaries <- bind_rows(summarised_cv_n20,
                                     summarised_cv_n40,
                                     summarised_cv_n60,
                                     summarised_cv_n80,
                                     summarised_cv_n100) %>%
    mutate(type = "test")

It looks like the more facilities we add, the better the coverage…mostly.

bound_training_summaries <- bind_rows(mc_cv_fit_n20$model_coverage,
                                      mc_cv_fit_n40$model_coverage,
                                      mc_cv_fit_n60$model_coverage,
                                      mc_cv_fit_n80$model_coverage,
                                      mc_cv_fit_n100$model_coverage) %>%
    mutate(type = "training")

bound_all_summaries <- bind_rows(bound_testing_summaries,
                                 bound_training_summaries)

ggplot(bound_testing_summaries,
       aes(x = n_fold,
               y = pct_cov,
               colour = factor(n_added),
               group = factor(n_added))) + 
    geom_point() + 
    geom_line() + 
    theme_minimal()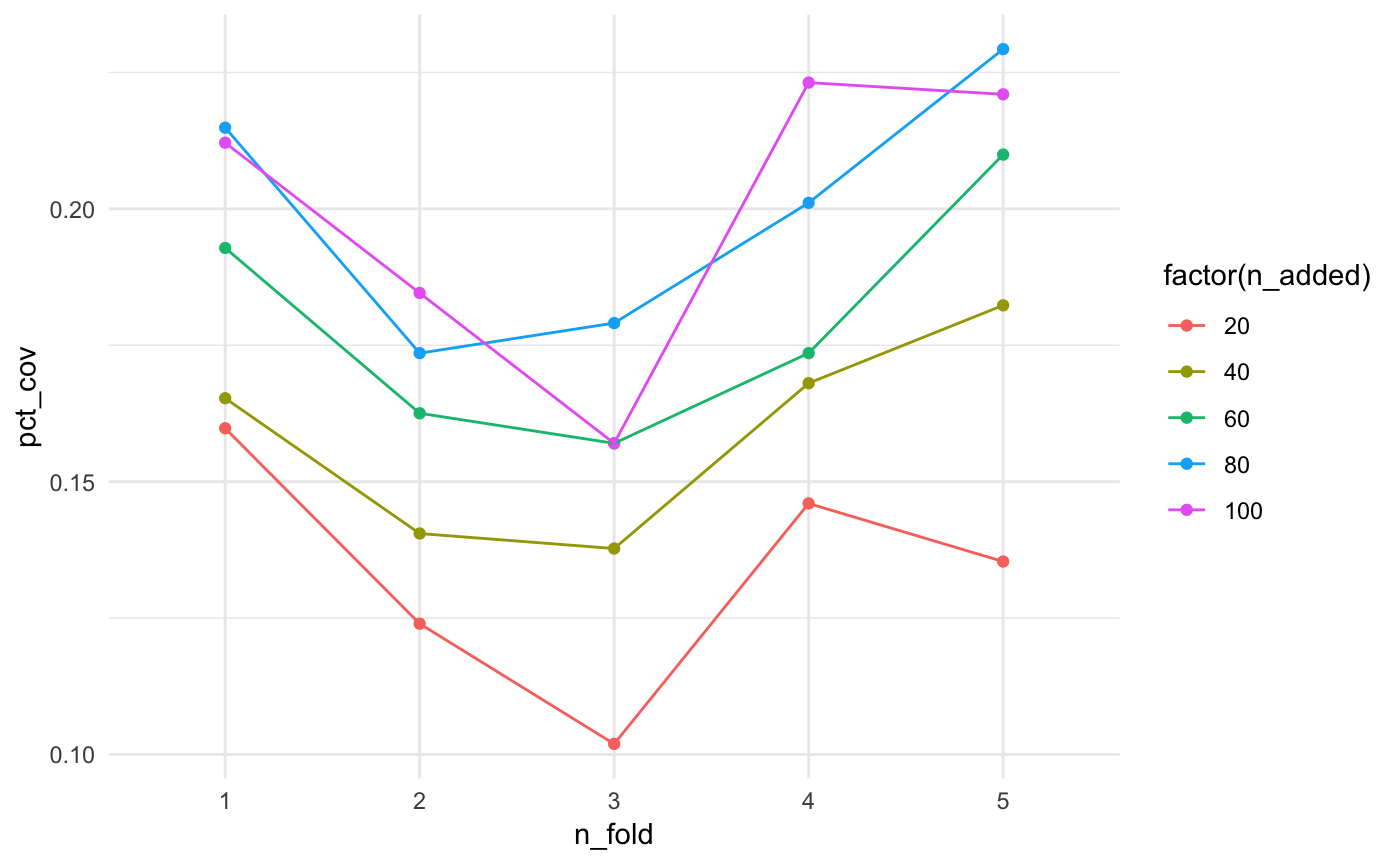

Let’s look at this another way, with boxplots for the number of facilities added.

ggplot(bound_testing_summaries,
       aes(x = factor(n_added),
           y = n_cov)) +
    geom_boxplot() + 
    theme_minimal()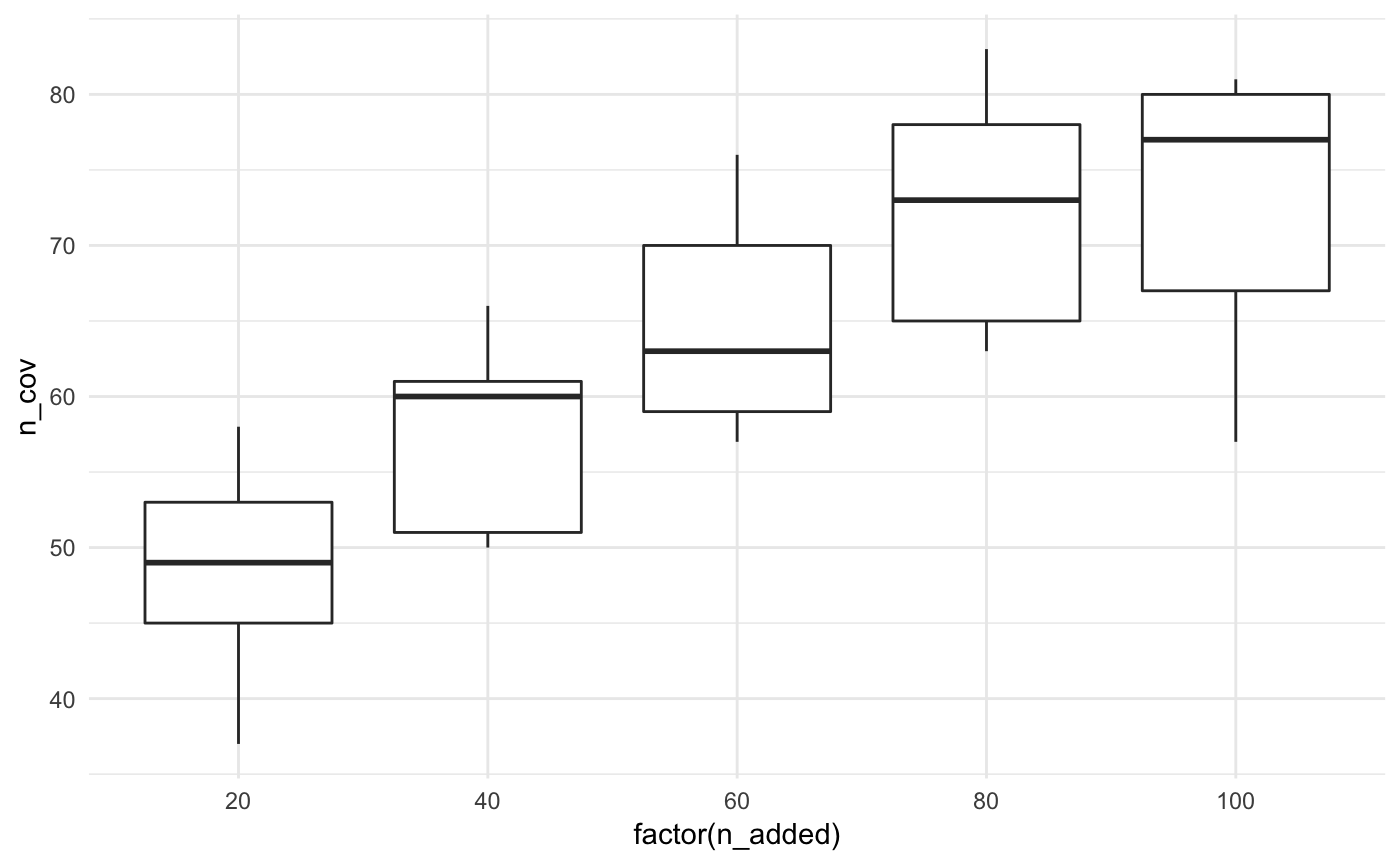

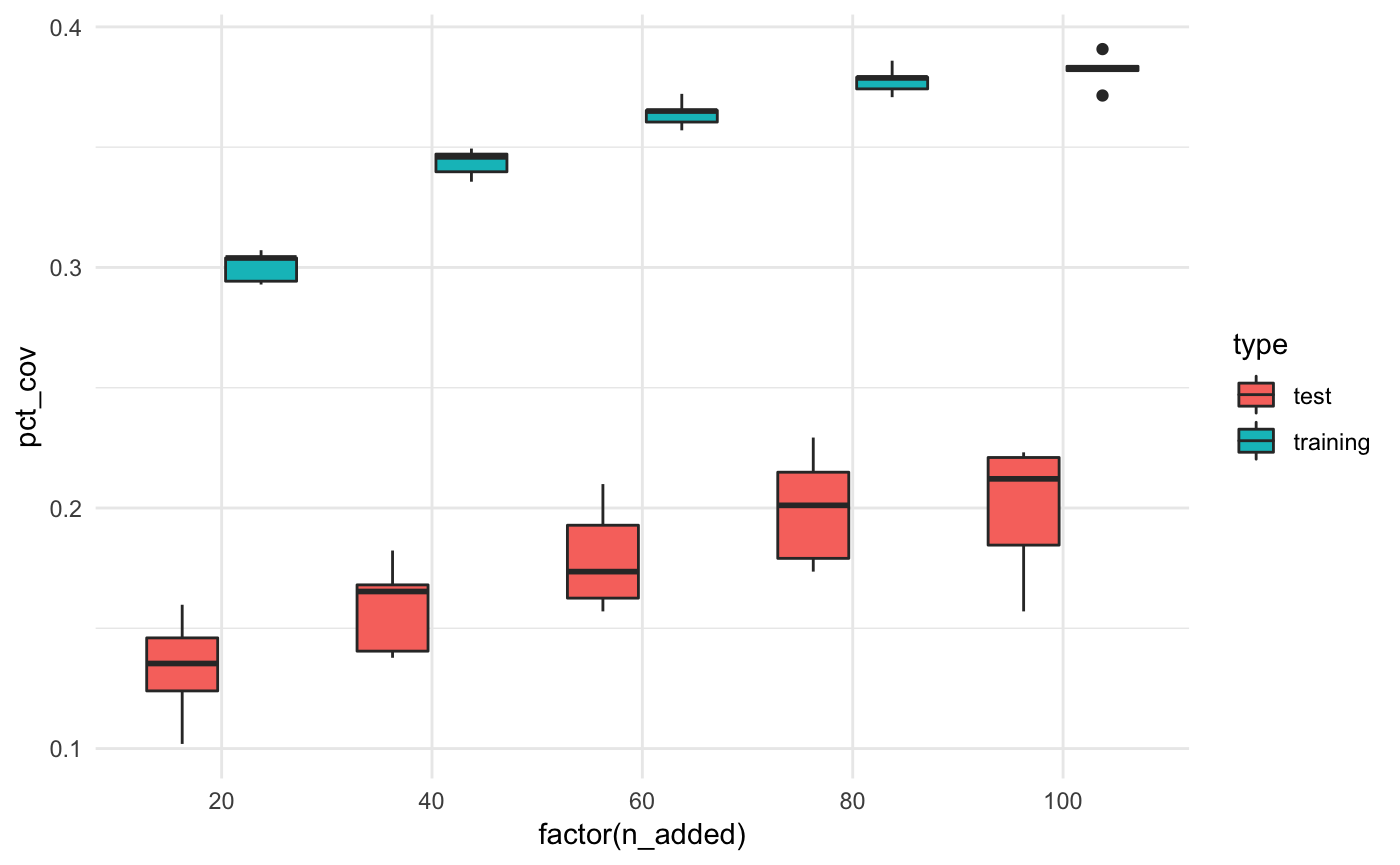
We can also compare the % coverage for the test and training datasets

bound_all_summaries %>%
    ggplot(aes(x = factor(n_added),
               y = pct_cov,
               fill = type)) + 
    geom_boxplot() + 
    theme_minimal()